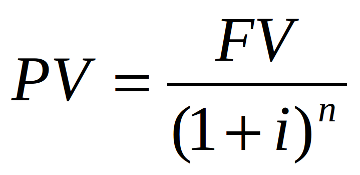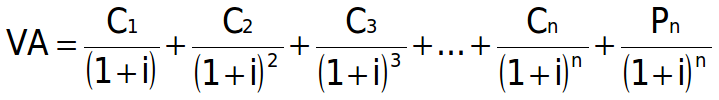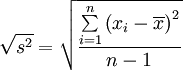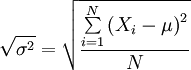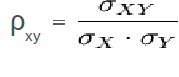¿Que debes saber para entender y aplicar el Valor en Riesgo?
Administración de Riesgos de IFIs Post Follow @juanbaeziINTRODUCCIÓN
Aquí revisamos algunos del los conceptos que debes manejar si quieres entender y usar Valor en Riesgo (VaR), todos estos conceptos están incorporados en la definición del VaR: determinación del valor o precio de activos o instrumentos financieros, cálculo de rendimiento, media, desviación estándar, Distribución Normal Estándar, intervalo de confianza, percentiles, covarianzas y correlaciones.
Iniciaremos con el Concepto de VaR:
CONCEPTO DE VAR.
El VaR mide la peor (máxima) pérdida esperada del valor de mercado de un solo activo financiero o una cartera de activos financieros en un periodo de tiempo determinado bajo condiciones normales del mercado ante un nivel de confianza dado. Ver Como Entender y Calcular el VaR
DETERMINACIÓN DE VALOR DE MERCADO
El método mas utilizado y aceptado es el Valor Actual del instrumento financiero.
La formula general de Valor Presente es:
Donde:
PV es el Valor Presente o Actual de un Instrumento financiero (préstamos, depósitos, bonos, letras del tesoro, etc.
FV es el Valor Futuro a recibir de un instrumento financiero, para el caso de los bonos son los cupones y el principal.
i es la tasa de descuento. También se le llama Retorno al Vencimiento (RAV) o simplemente TIR (Tasa Interna de Retorno)
Esta formula genera de Valor Actual o Presente transportado para el caso de un bono sin opciones queda así:
Donde:
Cn = pago cupón en el año n
Pn = principal devuelto en el “nº” año
i = bonos disponibles a la tasa de interés corriente con riesgo comparable (“tasa de descuento”).
CALCULO DE RENDIMIENTO DE UN ACTIVO FINANCIERO.
El calculo de los rendimientos de los precios para cada uno de los factores de precios de la siguiente forma:
Donde:
ln es el logaritmo natural
Pt es el precio actual o base
Pt-1 es el precio del periodo anterior (día, mes, etc)
MEDIA
Es la media aritmética o promedio, de una cantidad finita de números, es igual a la suma de todos ellos dividida entre el número de sumandos.
DESVIACIÓN ESTÁNDAR
También conocida como desviación típica es una medida de dispersión que informa de la media de distancias que tienen los datos respecto de su media aritmética, expresada en las mismas unidades que la variable.
Muestra
Población
PERCENTILES
Indica el valor que tiene la variable observada cuando se han acumulado un x% de observaciones colocadas en orden.
DISTRIBUCIÓN NORMAL
- Se dice que una distribución es normal (o se ajusta a una normal) cuando existe una alta probabilidad de que las observaciones se acerquen a la media y que la probabilidad sea simétricamente menor conforme se aleje de ella
- La Distribución Normal tiene la forma de una campana simétrica cuya media, mediana y moda coinciden en el mismo valor
- Es asintótica por naturaleza, pues nunca toca el eje horizontal
- La Distribución Normal puede ser descrita por dos datos, su media y su desviación estándar
DISTRIBUCIÓN NORMAL ESTÁNDAR
- Es aquella que tiene una media de 0 y distribución estándar de 1
- Las variables aleatorias pueden estar definidas en una variedad de unidades de medición: dólares, metros, minutos, etc.
- En el caso de la distribución normal estándar siempre son unidades estandarizadas (unidades de desviación estándar) y se representan en una sola distribución (valores z)
- Cualquier distribución Normal puede ser transformada a una distribución normal estándar, mediante la siguiente formula:

Donde:
Z es la unidad estandarizada de la desviación estándar calculada
X es el valor puntual de la variable observada
µ es la media de los valores de la variable observada
σ es la desviación estándar
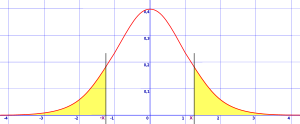
INTERVALOS DE CONFIANZA
Relación directa entre desviación estándar e intervalos de confianza de la distribución
Intervalo de confianza de dos colas
Intervalo de confianza de una cola
COVARIANZA
- Es un indicador que mide el grado en el que dos variables se mueven en línea.
- Una covarianza positiva indica que las variables se mueven en la misma dirección (atraen) y si es negativa que se mueven en direcciones opuestas (repelen)
- La formula de la covarianza es la sumatoria del producto de las dispersiones de las dos variables dividido para el número de observaciones:
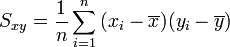
- No indica necesariamente que tan fuerte es la atracción entre las variables.
COEFICIENTE DE CORRELACIÓN
- Mide la fuerza y la dirección de una relación lineal entre dos variables aleatorias.
- Se considera que dos variables cuantitativas están correlacionadas cuando los valores de una de ellas varían sistemáticamente con respecto a los valores homónimos (coexistentes) de la otra.
- La correlación es un número entre +1 y -1
- No mide ni la volatilidad de alguna de las series ni indica necesariamente un sentido de causa y efecto.
- Se calcula utilizando la Correlación de Pearson: es la razón de dividir la covarianza de las dos variables para el producto de sus desviaciones estándar.
Etiquetado bajo
Cálculo de Rendimiento de un Activo Financiero Coeficiente de Correlación Covarianza desviación estándar Determinación de Valor de Mercado Distribución Normal Distribución Normal Estándar intervalo de confianza Percentiles Valor en Riesgo VaR